
Introducción
No se pueden promediar porcentajes porque se refieren a poblaciones distintas. No es lo mismo, p. ej., un 3% de una población de 100 (que son 3 unidades) que un 3% de una población de 1.000 (30 unidades).
Ejemplos
1)
Una biblioteca tiene 1.000 libros, y debido a una inundación varios libros se estropean. El personal de cada sección de la biblioteca cuenta cuántos libros se han deteriorado en su sección:
Sección | Stock de libros | Nº de libros deteriorados | % de libros deteriorados |
Física | 600 | 30 | 5 |
Matemáticas | 100 | 20 | 20 |
Medicina | 10 | 9 | 90 |
Sociología | 290 | 58 | 20 |
Sería erróneo calcular el % total de libros deteriorados a partir de los porcentajes parciales pues éstos corresponden a cantidades diferentes y, por tanto, tienen un peso distinto.
Erróneo: 5 + 20 + 90 + 20 = 135 135/4 = 33,75%
Correcto: 30 + 20 + 9 + 58 = 117 117/1000 = 0,117 o sea, un 11,7%
2)
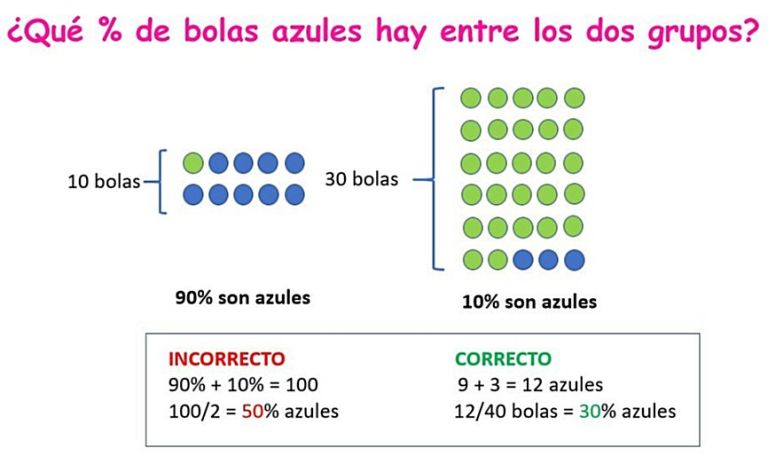
Conclusión
En resumen, si se promedian porcentajes sin considerar la base sobre la cual se calcularon, se obtienen resultados falsos.
No es correcto calcular promedios de promedios o promedios de porcentajes. En su lugar, hay que trabajar con los datos originales, y calcular promedios o porcentajes sobre el conjunto completo.
Tomàs Baiget
https://www.directorioexit.info/ficha46
